Maths – Fractal, Sierpinski Triangle Generation using the Chaos Game
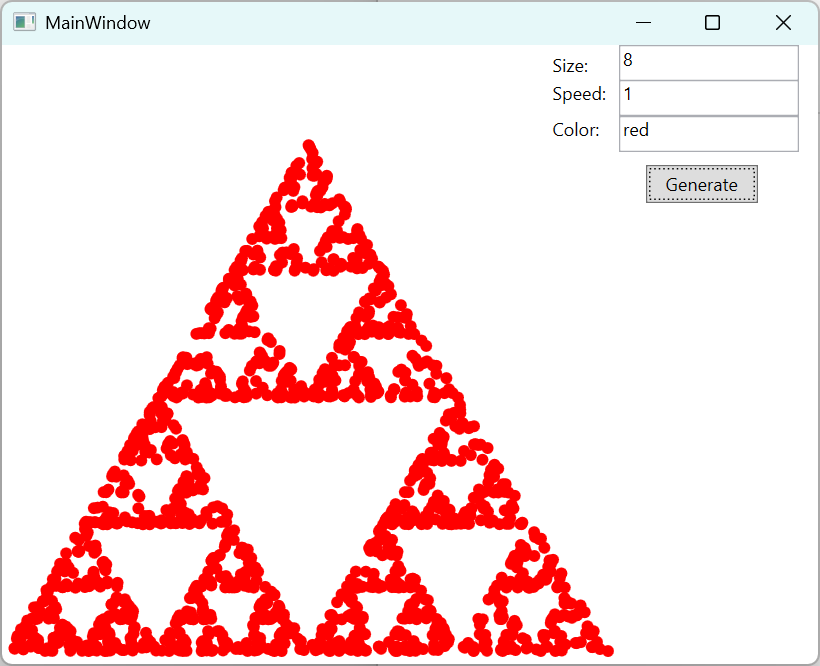
This simulation uses the Chaos Game to generate a fractal pattern. The circles placed to mark the locus of the points that form the fractal can have their sizes and color modified to generate a higher detail fractal. The simulation speed can also be changed accordingly.
The simulation was written in C#, WPF. The code works the following way: We take a triangle, and starting from it’s center, we pick a random vertex. We then half the distance to this vertex and put a dot to this place. In the next round we repeat this procedure. This will naturally generate a Sierpinski triangle.
Download
Download (Exe): TriangleExe.zip
Download (Source code): Sierpinski-Triangle.zip
Github respository
https://github.com/mrgyularabai/Sierpinski-TriangleScreenshot
What is the Sierpiński triangle
The Sierpiński triangle is a famous fractal: a geometric shape that repeats the same pattern at smaller and smaller scales. What it looks likeIt starts as a simple triangle. Then:
- Divide the triangle into 4 smaller congruent triangles
- Remove the middle one
- Repeat the process on each remaining triangle forever
The result is a lace-like triangle made of infinitely many smaller triangles.
Key properties
Self-similar: Every part looks like a smaller copy of the whole
Infinite perimeter, but
Zero area (as the process continues indefinitely)
Fractal dimension ≈ 1.585 (between a line and a plane)
How it can be created
There are several equivalent ways:
Recursive removal
Chaos Game (implemented in my code)
Cellular automata patterns (related to Pascal’s triangle mod 2)
Why it’s important
The Sierpiński Triangle is a classic example in fractal geometry. It can be used to study recursion, infinity, and complexity. It appears in computer graphics, mathematics education, and signal/antenna design.
