AI Inference Engine for LLMs in C#.Net

This page presents my large language model inference engine, which is written entirely in C#. It can run open weight Large Language Models (LLMs) that use the LLama3.2 1 Bilion parameter architecture. It can read and parse GGUF files, do the tokenization / detokeinzation and can print out the response returned by the large language model after executing all the layers. This inference engine is very close to being able to use hardware acceleration.

Download summary article (.docx): InferenceEngineDescription.docx
Download summary article (.pdf): InferenceEngineDescription.pdf

How does it work

To understand how AI inference works for LLMs check out my Youtube playlist:

YouTube: How Large Language Models work by Gyula Rabai
Link: https://www.youtube.com/watch?v=NSCmXxaNfEY&list=PLqaqTbyiL2djqfW0s9cXUgEm_nHYp-tIr

Download

Download (model file): Llama-3.2-1B-Instruct-f16.gguf (2.4 GB)
Save the model file to: C:\AIModels\Llama-3.2-1B-Instruct-f16.gguf

Download (exe): AI-Inference-Engine.zip (272 KB)
Run: LLMInference.exe

Github repository

Console version

The inference engine can be best tested through a simple console app. This version is uploaded to Github under the MIT license. This console app serves as a simple front-end that makes it possible to load GGUF model files and to run the inference on them.

The project contains the source code of all the functional components: GGUF file parsing, Tokenization, Embedding, RMSNorm, Groupped Multi-headed Attention, GLU, and the layer implementation to support proper forward propagation.

Note, that this version might feel very slow, as all computations are done on the CPU. I am currently working on hardware acceleration, to support NPUs and GPUs natively. You can read more about the current work "Stage 2" at the following URL: https://gyularabai.com/p_9125-stage-2-hardware-acceleration-in-ai-inference.html

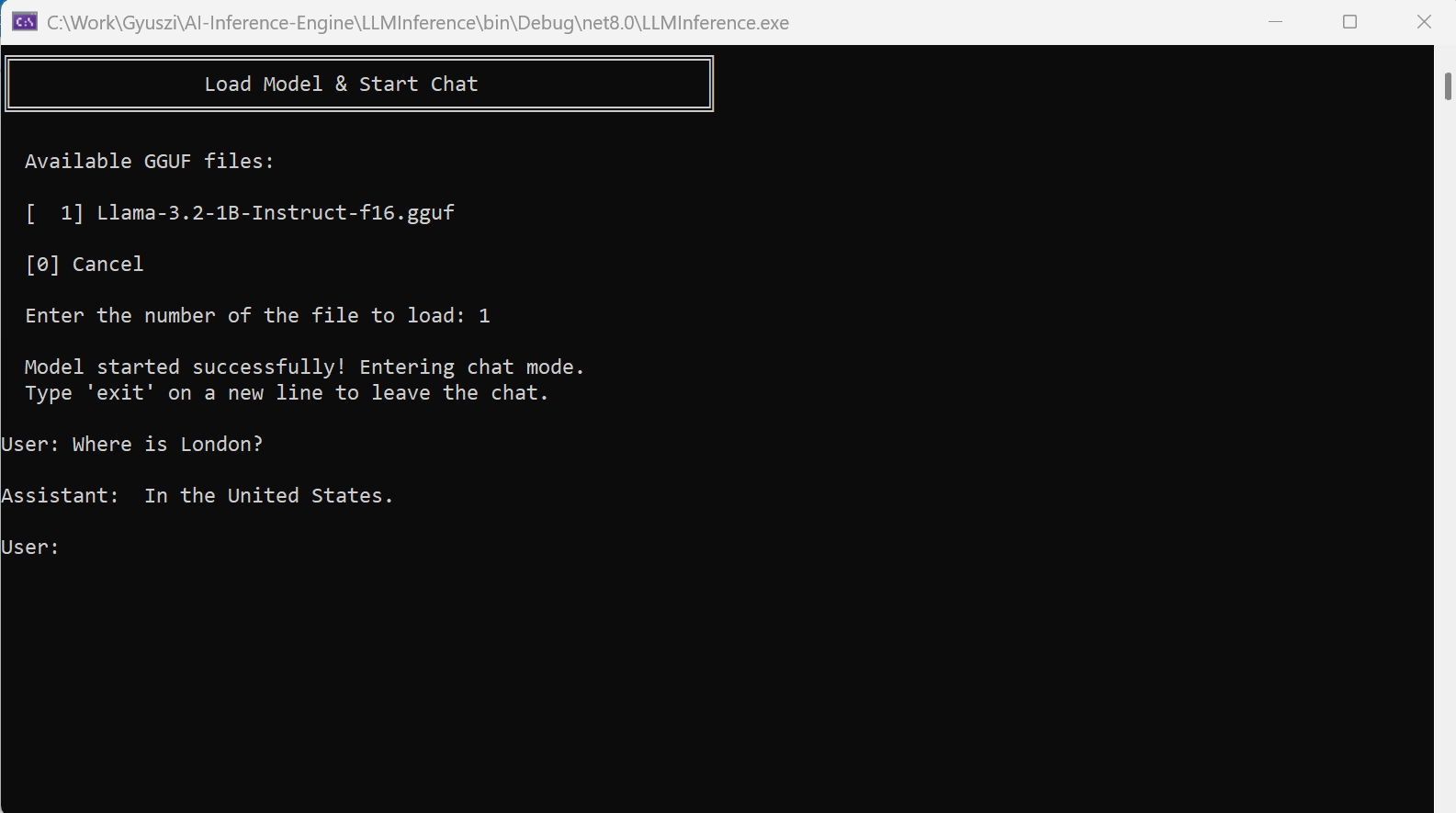
Video of placing breakpoints in the console version

To find the key steps in the LLM inference code, check out the following video. This video shows how to run the inference app in console mode with a debugger and where to set breakpoints to understand the key functional components.

Introduction

I designed and implemented a fully functional AI inference engine for large language models (LLMs) from scratch in C#. It is capable of running models implemented in the form of the Llama 3.2 architecture. It can parse models in the GGUF file format. The inference engine has a very flexible execution model that is easily adaptable to other architectures and is ready to implement row-level parallelism by distributing load to multiple processing units (CPUs, GPUs). With recent architectural changes it is also going to be able to efficiently utilize the respective memory hierarchies for each processing unit (System RAM, Caches, SSE registers, VRAM, and offloading to the SSD if required). Why Is This Contribution Unique

As far as I know, this is the first and only fully functional C# implementation of an LLM Inference engine.

Other solutions merely provide wrappers around calls to PyTorch or C++ implementations such as Georgi Gerganov’s llama.cpp . However, this approach limits the C# developer to only have access to the certain features exposed to them by the library, and fails to provide an inference framework, which can provide the practical flexibility that most applications demand. In my system, it is already easy to make modifications to the model architecture, execution platform or model type (quantization) across the entire AI stack, all of which is available in one place.

Lead-up project: Neural Network Simulator

Before I built my AI inference engine, I had written a neural network simulation that allowed me to simulate a small neural network. This project implements back-propagation for a small deep neural network (MLP) and also featured a visualizer to help me see how connections between neurons change in real-time with stochastic gradient descent optimization. My neural network simulator can be downloaded from this URL:
https://gyularabai.com/p_6410-neural-network-simulator.html

Motivation

I have learnt a lot about game development and I knew that modern video games work with very large amounts of data (several gigabytes) and can still run efficiently on relatively low-end GPUs. I know how these games use full utilization of the Graphics hardware available in Graphical Processing Units, which is heavily optimized for 4 by 4 matrices and 4 dimensional vectors as primitives. Furthermore, GPUs have a multistage pipeline that had been optimized for decades to deal with computation heavy graphics calculations, whereas, current approaches rely on trying to perform general computation (in compute shaders) on an otherwise heavily specialized processing unit. By considering the approaches used in game development much better AI execution frameworks could be written, which don’t rely on the hardware graphics manufacturers catering for both AI and graphics. Furthermore, I think the monopoly of the CUDA framework written by Nvidia can be broken by building a much better AI framework enabling other GPU manufacturers to contribute to the AI race.

Goals

Stage 1: Building a working AI inference engine in C#.Net, which correctly provides an abstraction between the AI model and the execution hardware running it. (Completed)

Stage 2: Implementing correct utilization of specialized hardware (GPUs, TPUs etc.) and a wider range of architectures. (In Progress)

Stage 3: Implement training and experiment with optimizing AI architectures.

Decisions and Development Environment

Why did I choose C#.Net? By the time I started this project I had written many pieces of code in Python, C# and various other software languages. Some of these projects are available at https://gyularabai.com. The current standard for AI is to use Python as proxy for complex C++ code. I myself have already built such a project with this kind of software stack: I built a Python game engine. Although it was great for rapid proto-typing, Python is not designed to easily stay performant and well organized for large projects. Therefore, I set about using C#, which provides much better support for object-oriented programming and still leaves room for high-performance. C# also has great interoperation capabilities with C++, allowing for the same, if not better performance optimization that the current AI software stack provides for.

In Visual Studio I could create a solution, that I could break down to subprojects, the sub projects could be broken down to classes, and large classes could be broken down to partial classes. I did not want to focus much effort on developing a GUI system from scratch, so I also used the .Net-based web-GUI framework developed in my father’s company.

Stage 1

Architectural Design

During the implementation of my AI inference engine I used the following architecture. This is the same architecture used by the LLama 3.2 AI model.

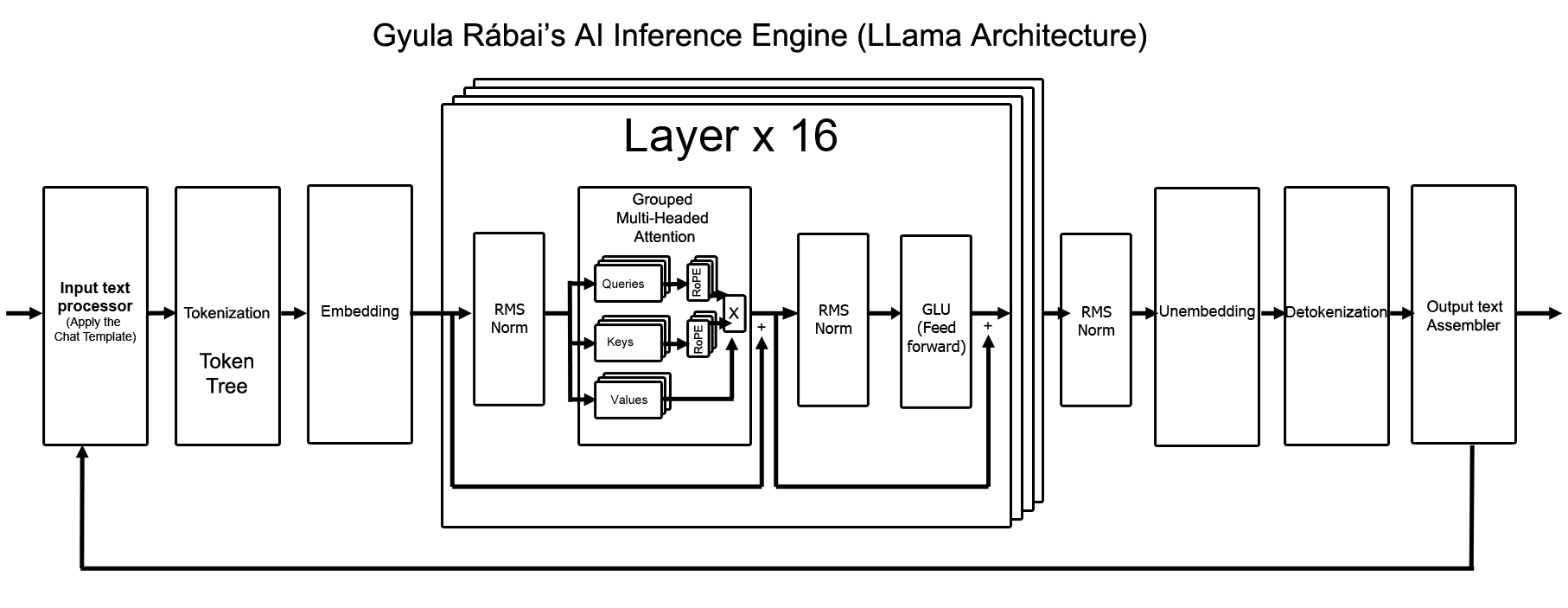
X: Scaled Dot Product Attention + Output Linear Transformation

Input Text Processing

My soltion can accept any text input. This tends to mean applying a chat-template which makes the text more akin to the environment the model was trained in.

Tokenization

The tokenization process relies on a few assumptions to implement a more performant approach than the traditional byte-pair-encoding (BPE) implentations:

1) Most token boundaries will fall on natural text boundaries such as word spaces and sentence ending periods.

2) Most longer tokens have a lower frequency than shorter tokens.

3) Even if a tokenization error occurs the model can still produce a usable output.

Assumption 3 is grounded in the fact that bigram models can still produce coherent text despite tokenization not accomodating for the natural meaning and structure of texts. Given this assumption, one can safely use a tokenization model that is only an approximation of what the full BPE merge rule-set would introduce and still get a very good output.

Assumptions number 1 and 2 garantee that a normal greedy approach to searching for tokens will either eventually self-correct (1) or produce the correct output regardless of ignoring merge-rules (2).

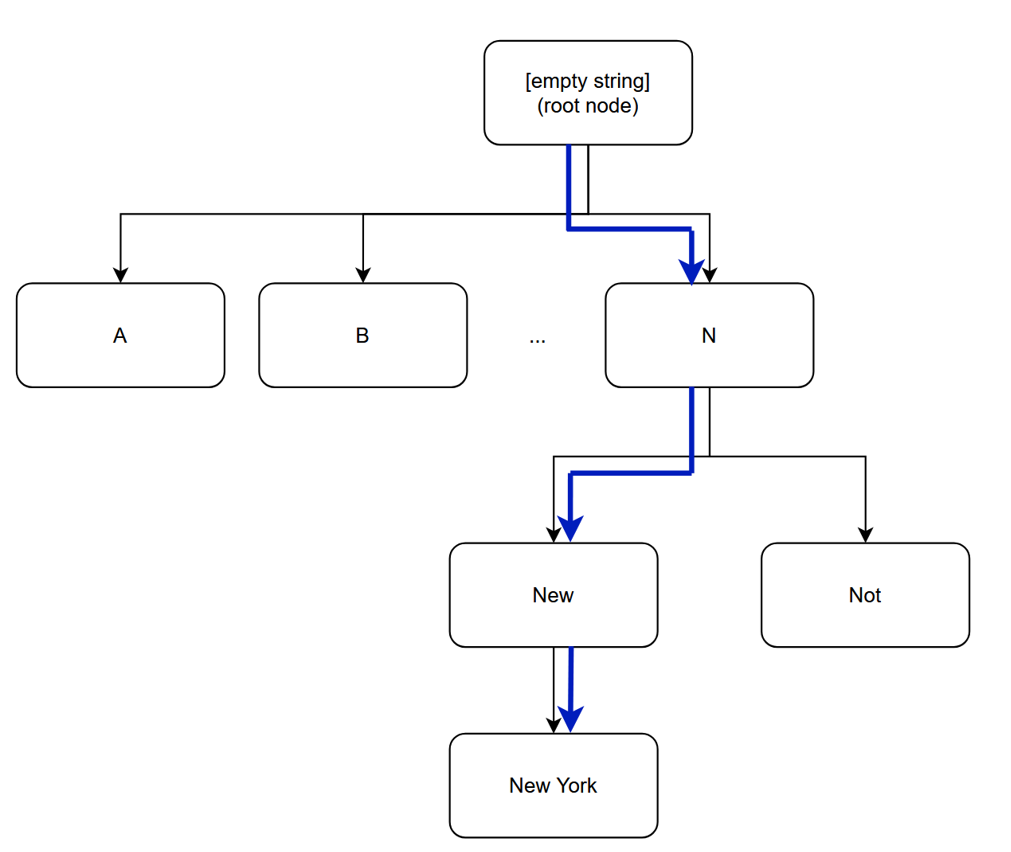
The approach I propose is as follows: one should build a token tree where one represents all possible tokens as a series of merges of previous tokens. Thus by traversing this B-Tree like structure whilst iterating over the characters of the text, one can achieve a linear time tokenization assuming that the decision at each branching of the tree is also linear time.

To make this approach even more efficient, it is sufficient to make each child node a continuation of the parent node where ’New’ is a continuation of ’N’. Then, as we natrually iterate through the caracters of the text, we can check whether a longer token is possible in the text (providing accuracy through assumption 2) or whether the text differs from the provided continuations which marks the end of the token (providing accuracy through assuption 1). The following figure illustrates an example of this so called Token Tree approach for tokenizing the word ’New York’ (part of the llama3 vocabulary):

For all the small scale test that I have performed, it has produced completely accurate results without any more pre- or post-processing required of the text at a sixfold increase in performance compared to llama.cpp’s traditional implementation in C++ (note that the GUI has a very limited refresh rate for the framework I am using). For the decisions at the branches, I use a hash-table (with taking the last few chars of each string as the hash), so that the amortized time complexity remains linear.

Embedding

This is the only part of the process that requires a vector of integers where the integers (int32) contain the token IDs generated through tokenization which also mark the indecies into what I represent as a list of vectors (the entire solution is broken down into vectors and matrices instead of tensors, so that higher parallelism may be achieved). This is contrary to the one-hot encoding appraoch where most of the matix is wastefully multiplied by 0s to yield a tensor to the same result.

RMS Normalization

This is the standard approach used where the RMS of the embedding vectors is calculated and then a division occurs. Of course, the hadamards product with a gain (float32) is also included. The entire operation must occur in 32-bit precision, because the reciprocal square root commonly used may go out of bounds for float16.

Attention

This is the standard grouped multi-headed operation, which forms the back bone of the transformer architecture. The embedding vectors are multiplied by a key and value martrix for each group which then contains multiple heads for the queries. The keys and queries go through a Rotary Postional Embedding (RoPE) operation before dot product attention is applied to them . The result is then concatenated for all the heads and transformed back into a set of vector which can be added to the residual stream.

GLU (Feed-Forward/MLP)

This is gated linear unit where vectors go through a non-linearity and a hadamard product. This typically happens in vectors 4 times the size of the orignials. To make this operation more efficient, I do not allocate a separate output ’tensors’ for each operation (lists of vectors), but rather I reuse the same memory for one of the two input matrix multiplications, the activation function, and the hadamard product.

Unembedding

This is the traditoinal matrix-multiplcation used to find the most similar vector to the last vector predicted by the sequence using the cosine similarity of the dot product. Then, the most similar token is chosen by taking the max value after a soft-max. Top-k, Top-p and temperature-based sampling is reserved for future implementations.

Detokenization

Output Text Processing

Other output processing may be applied if needed.

Technical Implementation

GGUF file parsing

The first step is to identify the metadata and load the model into RAM.

Metadata

The GGUF file represents meta-data through first containing a magic number (uint32, ASCII equivalent of ’G’, ’G’, ’U’, ’F’ unsuprisingly). Then a file-format version number is provided as well as with the count of how many tensors are stored. Finally, the number of metadata entries is given. Each metadata entry then follows suit.

The metadata entries all have a name (GGUF String), a type (enum of uint32), and a value. All strings start with a uint64 giving the string’s length and then a UTF-8 sequence. Other metadata types are relatively self-explanatory with a uint64 representing an unsigned 64-bit integer. An array of other metadata-entries is also possible (used for storing the token vocabulary). Perhaps the most notable metadata entry is the architecture which can be used to identify what other entries to expect.

This is then followed by headers for each tensor in the file. A header consists of a name (gguf string), an uint32 representing the dimension count, a series of uint64 s representing the dimensions of each tensors, finally a datatype for the tensor (enum) and a file offset is given.

The GGUF parser was a project in itself.

Tokenization

Tokenization was a project in itself. The solution I came up with to do this task efficiently is called TokenTree. Read more about it on the following page:

Inference

A nice way the core of the project is to take a look a the signature of the following function:

string Infer(string text)

This function takes in a prompt (text) and returns the next token the model predicts. This funciton is the heart of the system, as it actually does the inference:

OzAIModel_Ozeki _model;
string Infer(string text)
{
	OzLogger.Log(OzAILogger.LogSourceGy, LogLevel.Information, "Infer called with text: " + text);
	if (_model == null)
	{
		_model = new OzAIModel_Ozeki();
		_model.modelPath = GGUF.FileName;
	}
	
	try
	{
		_model.Start(out var error);
		if (error != null)
		return error;
		
		// Tokenization
		if (!_model.Tokenizer.GetTokens(text, out var inputTokens, out var times, out error))
		{
		return error;
		}
		
		// Inference
		if (!_model.infer(inputTokens, out var outputTokens, out var errorInfer))
		{
		return errorInfer;
		}
		
		var res = _model.Tokenizer.GetStringsRaw(outputTokens);
		return res;
	}
	catch (Exception ex)
	{
		return "Error: " + ex.Message;
	}
}

RMS Norm

Having spoken this much about RMS norm, let us take a look at its implementation. Firstly, all architecture components create their own OzAIArchComp class with its own IParams and HParams classes:

partial class OzAIRMSNorm
{

	public OzAICompIOMem_Unary Mem;
	
	public CompIParams IParams;
	public class CompIParams : OzAICompIParams
	{
		public OzAIScalar Part;
		public OzAIVector Gain;
		
		public override bool SetDefaults(OzAIProcMode mode, out string error)
		{
			if (!OzAIScalar.Create(1f, mode, out Part, out error))
			return false;
			error = null;
			return true;
		}
		
		public override bool IsPossible(out string error)
		{
			if (!CheckForExec(out error)) return false;
			List<object> objs = [Part, Gain];
			List<string> names = ["Part", "Gain Weights"];
			if (!CheckIfNull(objs, names, out error))
			return false;
			if (!Part.IsValid(out error))
			return false;
			
			if (!Part.Vector.GetNth(Part.Offset, out var partVal, out error))
			return false;
			
			if (partVal == 0)
			{
				error = "Cannot apply RMS to 0 elements of a vector.";
				return false;
			}
			
			return true;
		}
	}

	public CompHParams HParams;
	public class CompHParams : OzAICompHParams
	{
		public OzAIScalar Epsilon;
		
		public override bool SetDefaults(OzAIProcMode mode, out string error)
		{
			if (!OzAIScalar.Create(float.MinValue, mode, out Epsilon, out error))
			return false;
			error = null;
			return true;
		}
		
		public override bool IsPossible(out string error)
		{
			return CheckIfNull(Epsilon, "Epsilon", out error);
		}
	}
	
	public override bool IsPossible(out string error)
	{
		if (Params.Mem is not OzAICompIOMem_Unary)
		{
			error = "IO memory required to be in a format for a unary op.";
			return false;
		}
		
		if (Params.IParams is not CompIParams)
		{
			error = "Instance parameters required to be in a format for a OzAIRMSNorm.CompIParams.";
			return false;
		}
		
		if (Params.HParams is not CompHParams)
		{
			error = "Hyperparameters required to be in a format for a OzAIRMSNorm.CompHParams.";
			return false;
		}
		
		Mem = Params.Mem as OzAICompIOMem_Unary;
		IParams = Params.IParams as CompIParams;
		HParams = Params.HParams as CompHParams;
		
		error = null;
		return true;
	}
}

Vectors and scalars

The following classes are also key to the implementation:

The following page contains information about their implementation:

RMS Implementation

Finally, the actual forward function for the RMS Norm and thus the rest of the class is presented below:

public partial class OzAIRMSNorm : OzAIArchComp
{
	public override string Name => "OzAIRMSNorm";
	
	OzAIMemNode _f32Vecs;
	
	protected override bool InitInner(out string error)
	{
		_f32Vecs = new OzAIMemNode();
		error = null;
		return true;
	}
	
	public override bool Forward(out string error)
	{
		var exec = Params.IParams.ExecManager;

		if (!exec.GetProcMode(out var mode, out error))
		return true;

		if (!_f32Vecs.Clone(Mem.Inputs, out error))
		return false;

		var mem = _f32Vecs.GetArray();
		
		for (long i = 0; i < mem.LongLength; i++)
		{
			if (!mem[i].ToDType(OzAINumType.Float32, out mem[i], out error))
				return false;
		}
		
		if (!exec.RMS(HParams.Epsilon, IParams.Part, mem, mem, out error))
			return false;
		
		if (!exec.Had(mem, IParams.Gain, mem, out error))
			return false;
		
		var outs = Mem.Outputs.GetList();
		var outDtype = outs[0].GetNumType();
		
		for (int i = 0; i < (int)Mem.Outputs.Count; i++)
		{
			if (!mem[i].ToDType(outDtype, out var l, out error))
				return false;
			outs[i] = l;
		}
		error = null;
		return true;
	}
}

Breaking this apart, one extra memory node is required, because the RMS norm operation can only take place in float32. Therefore, the forward function clones the inputs into this memory node, converts them to float32.

if (!_f32Vecs.Clone(Mem.Inputs, out error))
	return false;

var mem = _f32Vecs.GetArray();

for (long i = 0; i < mem.LongLength; i++)
{
	if (!mem[i].ToDType(OzAINumType.Float32, out mem[i], out error))
	return false;
}

Then it asks the execution manager to perform the RMS:

if (!exec.RMS(HParams.Epsilon, IParams.Part, mem, mem, out error))
return false;

and apply the gain:

if (!exec.Had(mem, IParams.Gain, mem, out error))
return false;

Finally, it converts the results back to float16 and copies the result (shallowly) to the output mem node.

Embedding

Now that we have a basic grasp of the architecture of the code, I will move more quick onto the other architecture components to do an overview of how they each function. I will start with embedding. The CompParams are below:

partial class OzAIEmbedding
{
	public CompMem Mem;
	public class CompMem : OzAICompIOMem
	{
		public OzAIIntVec Input;
		public OzAIMemNode Outputs;
		public override bool IsPossible(out string error)
		{
			return CheckIfNull(Outputs, "Outputs", out error);
		}
	}

	public CompIParams IParams;
	public class CompIParams : OzAICompIParams
	{
		public OzAIVector[] Embeddings;
		
		public override bool IsPossible(out string error)
		{
			if (!CheckForExec(out error)) return false;
			return CheckIfNull(Embeddings, "Embeddings", out error);
			}
		}

	public override bool IsPossible(out string error)
	{
		if (Params.Mem is not OzAICompIOMem)
		{
			error = "IO memory required to be in a format for a unary op OzAIEmbedding.OzAICompIOMem.";
			return false;
		}
		if (Params.IParams is not CompIParams)
		{
			error = "Instance parameters required to be in a format for a OzAIEmbedding.CompIParams.";
			return false;
		}
		
		Mem = Params.Mem as CompMem;
		IParams = Params.IParams as CompIParams;
		
		error = null;
		return true;
	}
}

For IO, it takes an int vector in and returns a memory node. The only other parameter is the embedding vectors themselves. This component takes not hparams. The forward function is below:

public partial class OzAIEmbedding : OzAIArchComp
{
	public override string Name => "OzAIEmbedding";
	
	public override bool Forward(out string error)
	{
		var idxs = Mem.Input;
		if (!idxs.GetNumCount(out var len, out error))
		return false;
		
		var res = new OzAIVector[len];
		
		for (ulong i = 0; i < len; i++)
		{
			if (!idxs.GetNthInt(i, out var idx, out error))
			return false;
			var resVec = IParams.Embeddings[idx];
			if (!resVec.Clone(out res[i], out error))
			return false;
		}
		
		Mem.Outputs.Clear();
		Mem.Outputs.Add(res);
		
		error = null;
		return true;
	}
}

This iterates over each component of the int vector, indexes into the embedding vector list and clones the result it into the output memory node.

Attention

The attention component consists of multiple sub-components. It's iplementation is explained on the following page

RoPE

Although this is a primitive operation for the exec manager, I found it more convenient to extract it into its own component. I have to regretfully note that many fellow AI researchers failed to read the RoFormer paper to its conclusion. Not only are there as many different implementations as there are sections of the paper (presenting the RoPE they originally introduced with successively more efficient approaches), but also it is a coin flip as to whether the vectors are split down the middle and paired with the first element being paired with the one in the middle or whether the original approach of paring the first with the second etc. was taken. I do not look forward to implementing all the different versions in the future. No less, I have prepared for the possibility by making this its own component. Here are the CompParams:

public abstract class OzAIRoPE : OzAIArchComp
{
	public OzAICompIOMem_Unary Mem;
	
	public CompHParams HParams;
	public class CompHParams : OzAICompHParams
	{
		public OzAIScalar ThetaBase;
		
		/// <summary>
		/// Like part for RMS norm but instead of a percentage of the total number of dimensions, 

		/// the number of the first few dimensions is specified, for where rope should be applied.
		/// </summary>
		
		public uint DimCount;
		public OzAIRoPE_ScalingType Scaling = OzAIRoPE_ScalingType.Linear;
		public OzAIRoPE_Scaling.ScalingParams ScalingParams;
		
		public override bool SetDefaults(OzAIProcMode mode, out string error)
		{
			if (!OzAIScalar.Create(10000, mode, out ThetaBase, out error))
				return false;
			return true;
		}
		
		public override bool InitFromFile(OzAIProcMode mode, OzGGUFFile file, out string error)
		{
			// Base
			if (!file.GetMDFloat32($"{file.Architecture}.rope.freq_base", out var thetaBaseF, out error, false, 10000.0f) && error != null)
				return false;
			
			if (!OzAIScalar.CreateFloat(thetaBaseF, mode, out ThetaBase, out error))
				return false;
			
			// DimCount
			if (!file.GetMDUInt32($"{file.Architecture}.context_length", out var contextLen, out error))
				return false;
			
			if (!file.GetMDUInt32($"{file.Architecture}.embedding_length", out var embedLen, out error))
				return false;
			
			var defaultDimCount = embedLen / contextLen;
			if (!file.GetMDUInt32($"{file.Architecture}.rope.dimension_count", out DimCount, out error, false, defaultDimCount) && error != null)
				return false;
			
			// Scaling
			if (!OzAIRoPE_Scaling.ScalingParams.CreateFromFile(file, out ScalingParams, out Scaling, out error))
				return false;
			
			return true;
		}
		
		public override bool IsPossible(out string error)
		{
			if (!CheckIfNull(ThetaBase, "theta base", out error))
				return false;
			
			if (!ThetaBase.Vector.GetNth(ThetaBase.Offset, out var thetaBaseVal, out error))
				return false;
			
			if (thetaBaseVal < 0)
			{
				error = "Cannot calculate RoPE thetas with a base less than 0";
				return false;
			}
			
			if (thetaBaseVal == 0)
			{
				error = "Cannot calculate RoPE thetas with a base of 0 (this will always equal to 1)";
				return false;
			}
			
			if (DimCount == 0)
			{
				error = "Cannot calculate RoPE for 0 features of a vector";
				return false;
			}
			error = null;
			return true;
		}
	}

	OzAIRoPE_Scaling Scaling;
}

It is a unary op with no IParams. Its HParams are a DimCount as to how many dimensions will be used to form pairs of the original vector. The only scaling type for out of context tokens currently supported is linear, but this may change in the future. The scaling also has its own components. The theta base is also accepted. Here is the actual implementation:

/// <summary>
/// This type of RoPE is based on the original paper that proposed taking the 
/// consecutive elements as pairs for 2D rotation of theta * position radians where 
/// theta = Base^(di/2): d is the number of pairs of elements and i is the index 
//  of the pair of elements. 

/// </summary>
public class OzAIRoPE_Original : OzAIRoPE
{
	OzAIMemNode _f32Vecs;
	
	public override string Name => "OzAIRoPE_Original";
	
	protected override bool InitInner(out string error)
	{
	_f32Vecs = new OzAIMemNode();
	error = null;
	return true;
	}
	
	public override bool Forward(out string error)
	{
		var exec = Params.IParams.ExecManager;
		if (!exec.GetProcMode(out var mode, out error))
		return true;
		if (!_f32Vecs.Clone(Mem.Inputs, out error))
		return false;
		var mem = _f32Vecs.GetArray();
		for (long i = 0; i  < mem.LongLength; i++)
		{
			if (!mem[i].ToDType(OzAINumType.Float32, out mem[i], out error))
				return false;
		}
		
		if (!exec.RoPE(mem, HParams.ThetaBase, mem, out error))
			return false;
			
		var outputs = Mem.Outputs.GetList();
		var outDtype = outputs[0].GetNumType();
		
		for (ulong i = 0; i  < Mem.Outputs.Count; i++)
		{
			if (!mem[i].ToDType(outDtype, out var l, out error))
			return false;
			outputs[(int)i] = l;
		}
		error = null;
		return true;
	}
	
	public override bool IsPossible(out string error)
	{
		if (Params.Mem is not OzAICompIOMem_Unary)
		{
			error = "IO memory required to be in a format for a unary op OzAICompIOMem_Unary.";
			return false;
		}
		if (Params.HParams is not CompHParams)
		{
			error = "Hyperparameters required to be in a format for a OzAIRoPE.CompHParams.";
			return false;
		}
		
		Mem = Params.Mem as OzAICompIOMem_Unary;
		HParams = Params.HParams as CompHParams;
		
		error = null;
		return true;
	}
} 

This operation also requires conversion to float32, because sin and cos require more precision when rotating pairs. Otherwise, we just apply the primitive operation to the mem node.

GLU/MLP/Feedforward

Despite the many names this operation has, it is relatively straight forward. Here are the CompParams:

partial class OzAIGLU
{
	public OzAICompIOMem_Unary Mem;
	
	public CompHParams HParams;
	
	public class CompHParams : OzAICompHParams
	{
		public ulong FFNLength = 8192;
		
		public OzAICompHParams ActivationParams;
		
		public override bool IsPossible(out string error)
		{
			if (FFNLength == 0)
			{
				error = "Cannot compute a gated linear unit with 0 Feed Forward Length.";
				return false;
			}
			if (FFNLength >= int.MaxValue)
			{
				error = "Cannot compute a gated linear unit with Feed Forward Length greater than the max int 32 limit.";
				return false;
			}
			if (ActivationParams != null)
			{
				if (!ActivationParams.IsPossible(out error)) return false;
			}
			error = null;
			return true;
		}
	}
	
	public CompIParams IParams;
	
	public class CompIParams : OzAICompIParams
	{
		public OzAIMatrix WeightsTop;
		public OzAIMatrix WeightsGate;
		public OzAIMatrix WeightsBottom;
		public OzAIVector BiasTop;
		public OzAIVector BiasBottom;
		public OzAIActivation Activation;
		public OzAICompIParams ActivationParams;
		
		public override bool IsPossible(out string error)
		{
			List<object> objs = [ExecManager, Activation, ActivationParams, WeightsBottom, WeightsGate, WeightsTop];
			List<string> names = ["ExecManager", "Activation", "ActivationIParams", "WeightsBottom", "WeightsGate", "WeightsTop"];
			if (!CheckIfNull(objs, names, out error)) return false;
			if (!ActivationParams.IsPossible(out error)) return false;
			return true;
		}
	}
	
	public override bool IsPossible(out string error)
	{
		if (Params.Mem is not OzAICompIOMem_Unary)
		{
			error = "IO memory required to be in a format for a unary op OzAICompIOMem_Unary.";
			return false;
		}
		
		if (Params.IParams is not CompIParams)
		{
			error = "Instance parameters required to be in a format for a OzAIEmbedding.CompIParams.";
			return false;
		}
		
		if (Params.HParams is not CompHParams)
		{
			error = "Hyperparameters required to be in a format for a OzAIEmbedding.CompHParams.";
			return false;
		}
		
		Mem = Params.Mem as OzAICompIOMem_Unary;
		IParams = Params.IParams as CompIParams;
		HParams = Params.HParams as CompHParams;
		
		if (!IParams.WeightsGate.GetHeight(out var gateH, out error))
			return false;
	
		if (HParams.FFNLength != gateH)
		{
			error = "Feed forward length differs from the height of the gate weights matrix.";
			return false;
		}
		
		if (!IParams.WeightsTop.GetHeight(out var topH, out error))
			return false;
			
		if (HParams.FFNLength != topH)
		{
			error = "Feed forward length differs from the height of the top weights matrix.";
			return false;
		}
		
		if (!IParams.WeightsBottom.GetWidth(out var bottomW, out error))
			return false;
		
		if (HParams.FFNLength != bottomW)
		{
			error = "Feed forward length differs from the width of the bottom weights matrix.";
			return false;
		}
		
		error = null;
		return true;
	}
}

It is a unary op, and its HParams are the weights for the top vector (not passed into activation function), the ‘gate’ vector (passed into the activation function), the bottom vector (the one that comes out of the gate) and their respective biases if any. It also takes an activation component (currently a wrapper for the swish1 primitive op). It takes the feed-forward length (the size of the intermediate vectors) as the only HParam. Here is the implementation:

public partial class OzAIGLU : OzAIArchComp
{
	public override string Name => "OzAIGLU";
	
	// GateMem
	public OzAIMemNode GateOut;
	public OzAIMemNode Acc;
	
	protected override bool InitInner(out string error)
	{
		Acc = new OzAIMemNode();
		GateOut = new OzAIMemNode();
		
		var actMem = new OzAICompIOMem_Unary()
		{
		Inputs = GateOut,
		Outputs = GateOut
		};
		
		var compParams = new OzAICompParams()
		{
			Mem = actMem,
			IParams = IParams.ActivationParams,
			HParams = HParams.ActivationParams
		};
		
		if (!IParams.Activation.Init(compParams, out error))
			return false;
		
		return true;
	}
	
	public override bool Forward(out string error)
	{
		if (!InitMem(out error)) return false;
		if (!CalcTop(out error)) return false;
		if (!CalcGate(out error)) return false;
		if (!CalcBottom(out error)) return false;
		
		error = null;
		return true;
	}
	
	bool InitMem(out string error)
	{
		if (!Params.IParams.ExecManager.GetProcMode(out var mode, out error))
			return false;
			
		Acc.Clear();
		
		if (!Acc.AddVecs(mode, HParams.FFNLength, Mem.Inputs.Count, out error))
			return false;
		
		GateOut.Clear();
		
		if (!GateOut.AddVecs(mode, HParams.FFNLength, Mem.Inputs.Count, out error))
			return false;
			
		return true;
	}
	
	bool CalcTop(out string error)
	{
		var exec = Params.IParams.ExecManager;
		var inps = Mem.Inputs.GetArray();
		var acc = Acc.GetArray();
		
		if (!exec.MatMul(inps, IParams.WeightsTop, acc, out error))
			return false;
		
		var doBias = IParams.BiasTop != null;
		
		if (doBias && !exec.Add(acc, IParams.BiasTop, acc, out error))
			return false;
		
		return true;
	}
	
	bool CalcGate(out string error)
	{
		var exec = Params.IParams.ExecManager;
		var inps = Mem.Inputs.GetArray();
		var gateOut = GateOut.GetArray();
		var acc = Acc.GetArray();
		
		if (!exec.MatMul(inps, IParams.WeightsGate, gateOut, out error))
			return false;
			
		if (!IParams.Activation.Forward(out error))
			return false;
			
		if (!exec.Had(gateOut, acc, acc, out error))
			return false;
		
		return true;
	}
	
	bool CalcBottom(out string error)
	{
		var exec = Params.IParams.ExecManager;
		var inps = Mem.Inputs.GetArray();
		var acc = Acc.GetArray();
		var outs = Mem.Outputs.GetArray();
		
		if (!exec.MatMul(acc, IParams.WeightsBottom, outs, out error))
			return false;
		
		var doBias = IParams.BiasBottom != null;
		
		if (doBias && !exec.Add(outs, IParams.BiasBottom, outs, out error))
			return false;
		
		return true;
	}
}

This performs all the operations which are part of a gated linear unit. Swish1 requires float32 due to exp() operation it involves. No further comments.

Unembedding

Here are the CompParams:

partial class OzAIUnembedding
{
	public CompMem Mem;
	public class CompMem : OzAICompIOMem
	{
		public OzAIMemNode Inputs;
		public OzAIIntVec Output;
		public override bool IsPossible(out string error)
		{
			List<object> objs = [Inputs, Output];
			List<string> names = ["Inputs", "Output"];
			return CheckIfNull(objs, names, out error);
		}
	}

	public CompIParams IParams;
	public class CompIParams : OzAICompIParams
	{
	public OzAIVector[] Embeddings;
	
		public override bool IsPossible(out string error)
		{
			if (!CheckForExec(out error)) return false;
			eturn CheckIfNull(Embeddings, "Embeddings", out error);
		}
	}

	public CompHParams HParams;
	public class CompHParams : OzAICompHParams
	{
		public ulong VocabSize;
		
		public override bool IsPossible(out string error)
		{
			if (VocabSize == 0)
			{
				error = "Cannot compute unembeddings with a vocab size of 0.";
				return false;
			}
			error = null;
			return true;
		}
	}

	public override bool IsPossible(out string error)
	{
		if (Params.Mem is not OzAICompIOMem)
		{
			error = "IO memory required to be in a format for a OzAIUnembedding.OzAICompIOMem.";
			return false;
		}
		
		if (Params.IParams is not CompIParams)
		{
			error = "Instance parameters required to be in a format for a OzAIUnembedding.CompIParams.";
			return false;
		}
		
		if (Params.HParams is not CompHParams)
		{
			error = "Hyperparameters required to be in a format for a OzAIUnembedding.CompHParams.";
			return false;
		}
		
		Mem = Params.Mem as CompMem;
		IParams = Params.IParams as CompIParams;
		HParams = Params.HParams as CompHParams;
		
		if (HParams.VocabSize != (ulong)IParams.Embeddings.LongLength)
		{
			error = "Vocab size differs from the number of embeddings provided.";
			return false;
		}
		
		error = null;
		return true;
	}
} 

This includes the opposite of the embedding component, where the input is a mem node and the output is an int vector.

public partial class OzAIUnembedding : OzAIArchComp
{
	public override string Name => "OzAIUnembedding";
	
	public override bool Forward(out string error)
	{
		var exec = Params.IParams.ExecManager;
		if (!exec.GetProcMode(out var mode, out error))
			return false;
		
		var inps = Mem.Inputs.GetArray();
		var last = inps.Last();
		if (!OzAIVectorRange.Create(mode, HParams.VocabSize, out var scores, out error))
			return false;
		
		var inputs = new OzAIVector[HParams.VocabSize];
		for (ulong i = 0; i < HParams.VocabSize; i++)
		{
			inputs[i] = last;
		}
		
		if (!exec.Dot(inputs, IParams.Embeddings, scores, out error))
			return false;
		
		if (!OzAIScalar.CreateInt(0, mode, out var idx, out error))
			return false;
		
		if (!exec.Max(scores, idx, out error))
			return false;
		
		Mem.Output = (OzAIIntVec)idx.Vector;
		
		error = null;
		return true;
	}
}

This performs the dot product and then takes the max value which would also be the max value after the softmax. Thus, we obtain a single output integer which gives the next token.

Brining it all together

With this we have discussed all the architecture components used in the llama3 architecture apart from the layer itself.

Llama Layer

The code for both the parameters and the rest of the class is below without further discussion. The only thing of note it does other than calling all the subcomponents, is adding in the residual connections to where they need to go.

partial class OzAILayer_LLama
{
	public OzAICompIOMem_Unary Mem;
	public CompIParams IParams;
	public class CompIParams : OzAICompIParams
	{
		public OzAIRMSNorm.CompIParams AttnNorm;
		public OzAIMultiHeadAttn.CompIParams Attn;
		public OzAIRMSNorm.CompIParams GLUNorm;
		public OzAIGLU.CompIParams GLU;
		
		public override bool IsPossible(out string error)
		{
			List<object> objs = [AttnNorm, Attn, GLUNorm, GLU];
			List<string> names = ["AttnNorm", "Attn", "GLUNorm", "GLU"];
			if (!CheckIfNull(objs, names, out error))
			return false;
			
			if (!AttnNorm.IsPossible(out error)) return false;
			if (!Attn.IsPossible(out error)) return false;
			if (!GLUNorm.IsPossible(out error)) return false;
			if (!GLU.IsPossible(out error)) return false;
			
			return true;
		}
	}

	public CompHParams HParams;
	public class CompHParams : OzAICompHParams
	{
		public OzAIRMSNorm.CompHParams Norm;
		public OzAIMultiHeadAttn.CompHParams Attn;
		public OzAIGLU.CompHParams GLU;
		
		public override bool IsPossible(out string error)
		{
			List<object> objs = [Attn, Norm, GLU];
			List<string> names = ["Attn", "Norm", "GLU"];
			if (!CheckIfNull(objs, names, out error))
			return false;
			
			if (!Norm.IsPossible(out error)) return false;
			if (!Attn.IsPossible(out error)) return false;
			if (!GLU.IsPossible(out error)) return false;
			
			return true;
		}
	}

	public override bool IsPossible(out string error)
	{
		if (Params.Mem is not OzAICompIOMem_Unary)
		{
			error = "IO memory required to be in a format for a unary op OzAICompIOMem_Unary.";
			return false;
		}
		
		if (Params.IParams is not CompIParams)
		{
			error = "Instance parameters required to be in a format for a OzAILayer_LLama.CompIParams.";
			return false;
		}
		
		if (Params.HParams is not CompHParams)
		{
			error = "Hyperparameters required to be in a format for a OzAILayer_LLama.CompHParams.";
			return false;
		}
		
		Mem = Params.Mem as OzAICompIOMem_Unary;
		IParams = Params.IParams as CompIParams;
		HParams = Params.HParams as CompHParams;
		
		error = null;
		return true;
	}
}

Here is the rest of the class:

/// <summary>
/// This contains all the components of an LLama3.2 layer 
/// VectorWeights:
/// - AttnNorm
/// - RoPE Frequencies
/// - FFNNorm
/// - FFNBiases (Optional)
/// MatrixWeights:
/// - Attn
/// - FFN
/// </summary>
public partial class OzAILayer_LLama : OzAIArchComp
{
	public OzAIMemNode Acc;
	public OzAIMemNode AttnRes;
	
	public OzAIRMSNorm AttnNorm;
	public OzAIMultiHeadAttn Attn;
	public OzAIRMSNorm GLUNorm;
	public OzAIGLU GLU;
	
	public override string Name => "OzAILayer_LLama";
	
	protected override bool InitInner(out string error)
	{
		Acc = new OzAIMemNode();
		AttnRes = new OzAIMemNode();
		
		if (!createAttnNorm(out error)) return false;
		if (!createAttn(out error)) return false;
		if (!createGLUNorm(out error)) return false;
		if (!createGLU(out error)) return false;
		
		return true;
	}
	
	bool createAttnNorm(out string error)
	{
		AttnNorm = new OzAIRMSNorm();
		
		var attnNormMem = new OzAICompIOMem_Unary()
		{
			Inputs = Mem.Inputs,
			Outputs = Acc,
		};
		
		var attnNormParams = new OzAICompParams()
		{
			Mem = attnNormMem,
			IParams = IParams.AttnNorm,
			HParams = HParams.Norm
		};
		
		if (!AttnNorm.Init(attnNormParams, out error))
			return false;
		
		error = null;
		return true;
	}
	
	bool createAttn(out string error)
	{
		Attn = new OzAIMultiHeadAttn();
		
		var attnMem = new OzAICompIOMem_Unary()
		{
			Inputs = Acc,
			Outputs = Acc,
		};
		
		var attnParams = new OzAICompParams()
		{
			Mem = attnMem,
			IParams = IParams.Attn,
			HParams = HParams.Attn
		};
		
		if (!Attn.Init(attnParams, out error))
			return false;
		
		error = null;
		return true;
	}
	
	bool createGLUNorm(out string error)
	{
		GLUNorm = new OzAIRMSNorm();
		
		var GLUNormMem = new OzAICompIOMem_Unary()
		{
			Inputs = AttnRes,
			Outputs = Acc,
		};
		
		var GLUNormParams = new OzAICompParams()
		{
			Mem = GLUNormMem,
			IParams = IParams.GLUNorm,
			HParams = HParams.Norm
		};
		
		if (!GLUNorm.Init(GLUNormParams, out error))
			return false;
		
		error = null;
		return true;
	}
	
	bool createGLU(out string error)
	{
		GLU = new OzAIGLU();
		
		var GLUMem = new OzAICompIOMem_Unary()
		{
			Inputs = Acc,
			Outputs = Acc,
		};
		
		var GLUParams = new OzAICompParams()
		{
			Mem = GLUMem,
			IParams = IParams.GLU,
			HParams = HParams.GLU
		};
	
		if (!GLU.Init(GLUParams, out error))
			return false;
		
		error = null;
		return true;
	}
	
	public override bool Forward(out string error)
	{
		if (!initMem(out error)) return false;
		if (!attnBlock(out error)) return false;
		if (!gluBlock(out error)) return false;
		
		return true;
	}
	
	bool initMem(out string error)
	{
		if (!Acc.CreateDestOf(Mem.Inputs, out error))
		return false;
		if (!AttnRes.CreateDestOf(Mem.Inputs, out error))
		return false;
		return true;
	}
	
	bool attnBlock(out string error)
	{
		if (!AttnNorm.Forward(out error))
		return false;
		if (!Attn.Forward(out error))
		return false;
		
		var exec = IParams.ExecManager;
		var ins = Mem.Inputs.GetArray();
		var acc = Acc.GetArray();
		var attnRes = AttnRes.GetArray();
		
		if (!exec.Add(ins, acc, attnRes, out error))
		return false;
		
		return true;
	}
	
	bool gluBlock(out string error)
	{
		if (!GLUNorm.Forward(out error))
		return false;
		if (!GLU.Forward(out error))
		return false;
		
		var exec = IParams.ExecManager;
		var acc = Acc.GetArray();
		var attnRes = AttnRes.GetArray();
		var outs = Mem.Outputs.GetArray();
		
		if (!exec.Add(attnRes, acc, outs, out error))
		return false;
		
		return true;
	}
}

Detokenization

This is a trivial implementation of finding the correct OzAIToken from a list in the tokenizer class by indexing and returning it. However, before we move on from the technical implementation, I would also like to take a moment to consider how the primitive operations are executed.

Execution Manager

The execution manager manages, so called executors, which implement how to perform all the primitive vector operations on one set of hardware for one kind of datatype.

The execution manager's functionality is explained here:

The execution manager of Gyula Rabai's AI inference engine.

Challenges And Difficulties

Throughout this project, I encountered many difficulties and challenges along the way

Working Blindfolded (Biggest challenge): Before, having implemented it all, I was effectively programming blindfolded, having no way to tell whether the code I wrote would work or not. This is because everything had to be in place before the string going into the infer function could produce a string to come out the other end. Most people would give up on this because the uncertainty and lack of any feedback for months can absolutely destroy motivation.

Testing Blindfolded: After working for 4 months , I was not at all surprise when I found out that my code would not work first try. To the contrary, I was very surprised by the float32.NaN (not a number) that would randomly crop up in my solution. These came down to me forgetting to add the epsilon to the RMS norm (not believing it would make a difference). Hunting down countless more errors like this was a very exhausting process, because often the only feedback I would get is that the wrong token is coming out, and I have not the slightest idea why.

No Pen and Paper Verification: Even the “relatively small” large language model I used for development the Llama3, 1B model with 16-bit precision had over a billion parameters to use in the calculations. There was no way I could manually verify my calculations using the pen-and-paper method or simple calculators.

Hidden Pitfalls Not Talked About: Converting a float16 to a float32 seems like an obvious lossless operation. Not in AI. Conversions between data types even going from less to more precision often leads to unintended results and errors. Although, I thought I could skip steps in my implementation by converting everything to float32 and having to implement only one kind of executor. However, no one on the internet ever mentioned that this would lead to an ‘error’ of +/- 0.4 building up compared to the float16 implementation on all my values which was just big enough for all the output tokens to be nonsense. There were many more hidden pitfalls like this, which are not commonly talked about.

The Code Has to Start Optimized: During development, hardware optimizations, such as offloading calculations to GPUs, implementing AVX, or even CPU multithreading is just not an option, as the code is not in a stage to be optimized. This means, that every run is done by the CPU on one thread, and doing the calculations sequentially for a 1B parameter model is very-very time consuming. Often, I had to wait half an hour or an hour to know if I made an error. (To make things even worse, I often worked on my laptop at school in between classes, during lunch breaks or study time, and my laptop’s weaker hardware could not complete the test runs in the available time slot.) The only way to test the program was to write even more code without feedback to make it make it optimized enough to run under an acceptable amount of time. For me this was implementing multithreading.

Large Language Models are Just Too Big: the limit for the size of a list in C#, by virtue of the indexing operator only being implemented for int32, is exactly two gigabytes. When Microsoft wrote that the garbage collector is not a deterministic program, they were serious, because not matter what I tried I could not get my dead 1GB arrays to be removed from the large object heap. Large Language models are too big for conventional programming and optimizations have to be carefully considered to make handling such a large amount of data possible.

The necessary math is not taught in school: Even now, the furthest I was taught despite doing A-Level Further Mathematics and the Advanced Extension Award for Mathematics was that a vector is a list of numbers. That is fine for doing 3D geometry calculations, but when your tensor has 12x16x4x1024 dimensions, things get serious. I had to learn all of the relevant Mathematics on my own.

No reference projects or ready to use components were available in C#: In the AI world, everything is written in Python or C/C++. There are no C# implementations of ready to use components available. I had to design and implement every component from scratch. Furthermore, I had no einsum! That means I had to visualize the rank 5 tensor operations used for grouped multi-headed attention and figure out what its vector equivalent was. The only guidance I received looked like this ‘torch.einsum(“bchd, hgd -> bcgd”, tensor1, tensor2, tensor3)’.

The question of “why” is often not answered: Many research papers discuss results reached based on trial and error and the authors fail to discuss or analyze why it works. When I had “why” questions, for example “Why rotate pairs for positional encoding” it was often not trivial to reach the answer.

No peer or teacher support: I didn’t have help. I could only turn to the Internet if didn’t understand something. I occasionally could discuss some issues with university students over Discord, who were just as confused as I was.

Key findings / What did I discover along the way

Existing implementations (mainly in Python and C++) of functional components are often far from optimal. Better data models and better algorithms could significantly increase the efficiency of current AI systems. (For example, the tokenizer I designed, which I call “TokenTree” works at 6x efficiency over existing implementations)

Everybody is using already available components in Python, so errors created by early researchers, and early developers are built into later projects (like optimizing blas for square matrices whereas modern AI tensor operations come in all shapes and forms). People build on components with errors without knowing.

Current LLM engines use the Nvidia CUDA framework and often use primitive data distribution models, if we go one layer deeper and work directly with GPUs, NPUs and CPUs we can build better systems.

There is a lot of noise in this reasearch field. Not every research paper is reproducable, and one often encounters explanatory articles, which use highly-technical terminology to confuse the reader.

Stage 2

This is the stage I am currently working on. The current progress can be viewed on the following URL:

Stage 3

Future Roadmap

The next stage is to add GPU, NPU, AVX2 and AVX512 support. This takes also requires improving the software infrastructure to support a new new device-less memory model, which will allow me to offload work onto this accelerators.

The next stage will be to expand the number of architectures I support, create a better file format, which stores not only the model weights but also the model specific architecture, and hopefully surpass state-of-the-art execution systems with my innovations, one step at a time!

Sharing the Knowledge

It has been an incredible journey so far and I have learnt a lot along the way. Therefore, I am also putting a lot of effort into sharing the knowledge I have acquired during this project. There are 3 things I do:

I hold lectures on he topic for interested societis and classes. Some of them can be found on the following URL
https://gyularabai.com/p_9109-presentations.html

I have created a youtube video seriest to explain how LLMs work
https://gyularabai.com/p_8677-ai-lectures.html

I am working on a book to help others who want to understand the topic deeper.
https://gyularabai.com/p_8866-create-a-large-language-model-hands-on-guide.html